University Brain

Search

SearchSearch

MistralAI

Sep 01, 2024, 3 min read

00 Алгебра и геометрия

Ответы сгенерированы MistralAI

Используйте на свой страх и риск

  1. Определение поля (аксиомы входят в определение)

  1. Определение линейного пространства над полем (аксиомы входят в определение)

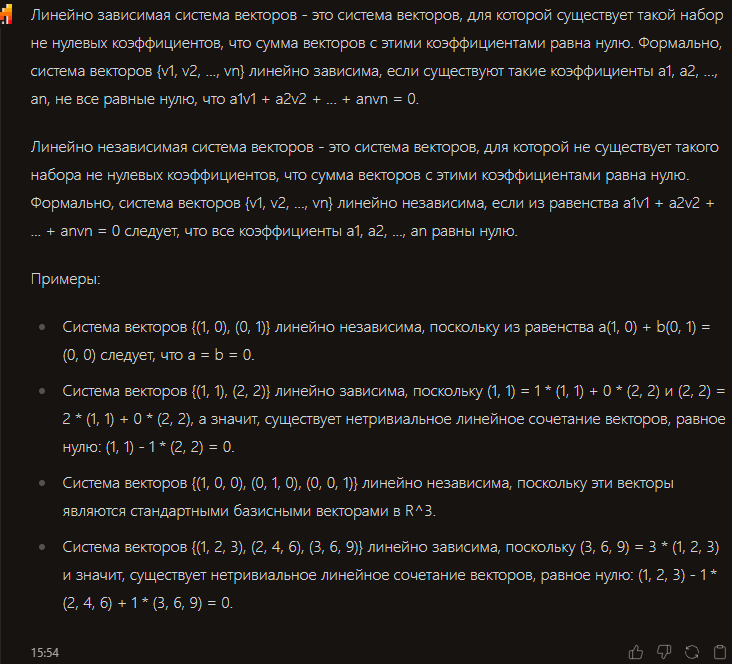
  1. Определение линейно зависимой системы векторов, определение линейно независимой системы векторов, привести примеры

  1. Определение базиса линейного пространства, определение размерности линейного пространства, определение координат вектора в базисе

  1. Матрица перехода Определение, вывод формул, связывающих координаты вектора в старом базисе с его координатами в новом базисе

  1. Определение изоморфных линейных пространств Привести примерыСвойства изоморфизма (рефлексивность, симметричность, транзитивность) Доказательство

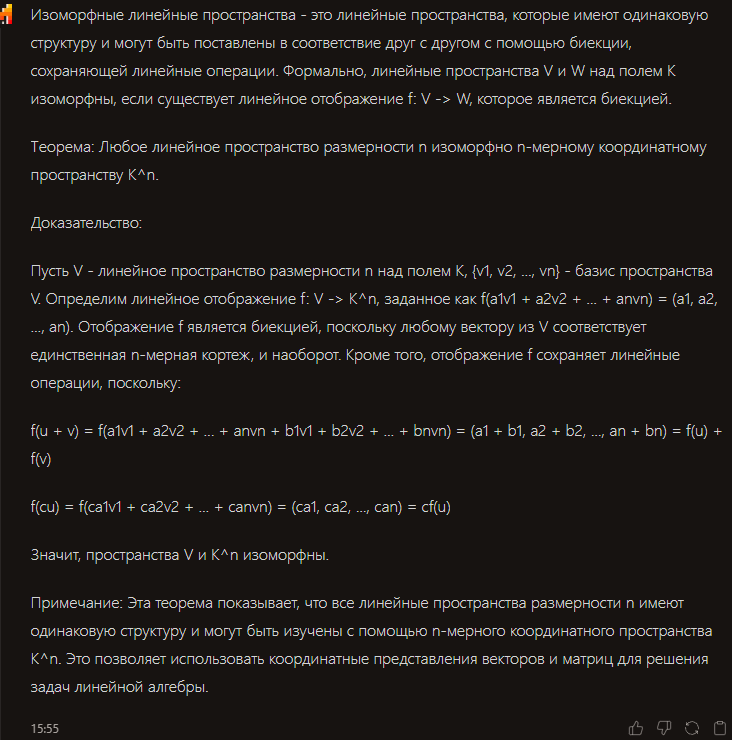
  1. Определение изоморфных линейных пространствДоказать теорему о том, что любое пространство размерности n изоморфно n-мерному координатному пространству

  1. Определение подпространства линейного пространства Эквивалентное определение

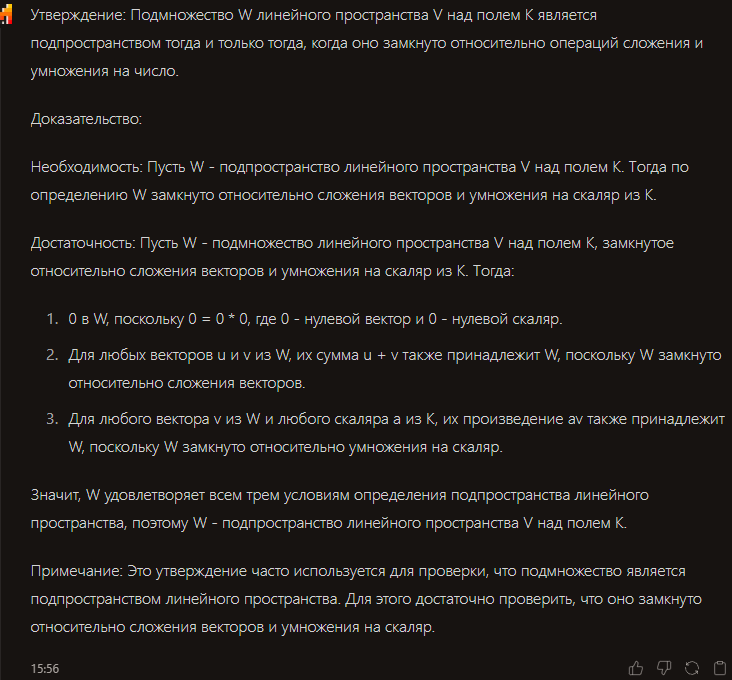
  1. Доказательство утверждения, что подмножество является подпространством тогда и только тогда, когда оно замкнуто относительно операций сложения и умножения на число

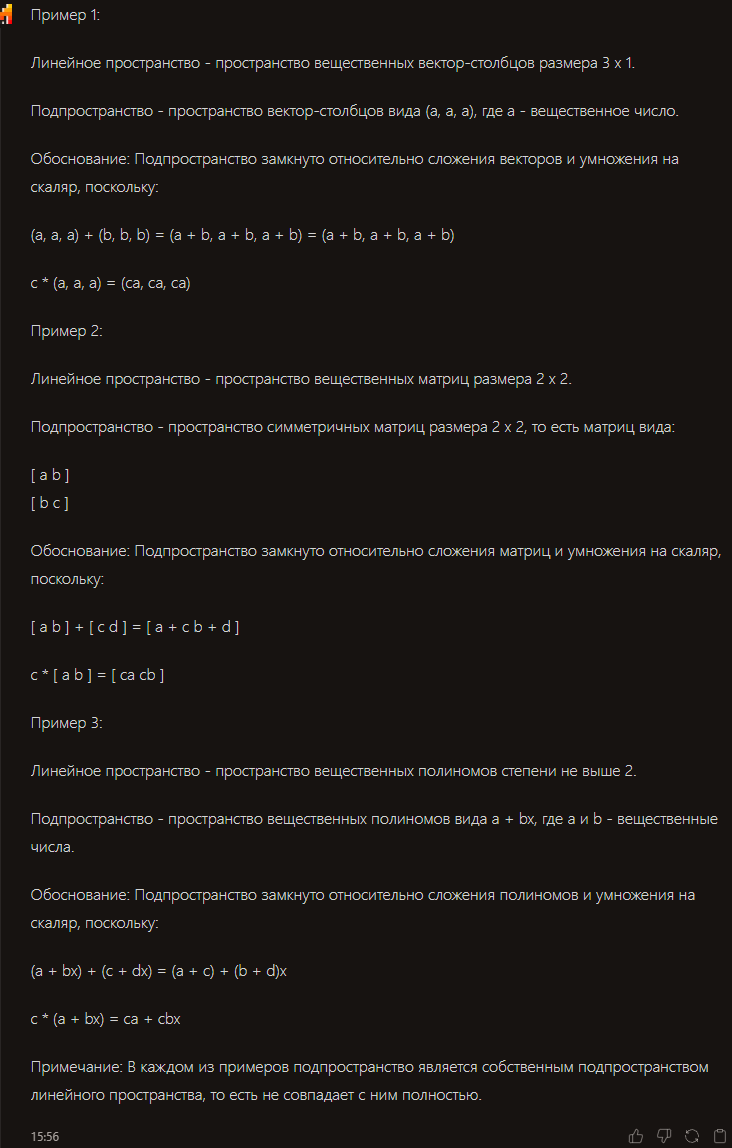
  1. Привести несколько примеров линейного пространства и его подпространства Обосновать

  1. Определение суммы и пересечения двух подпространств

  1. Определение прямой суммы подпространств Привести несколько примеров

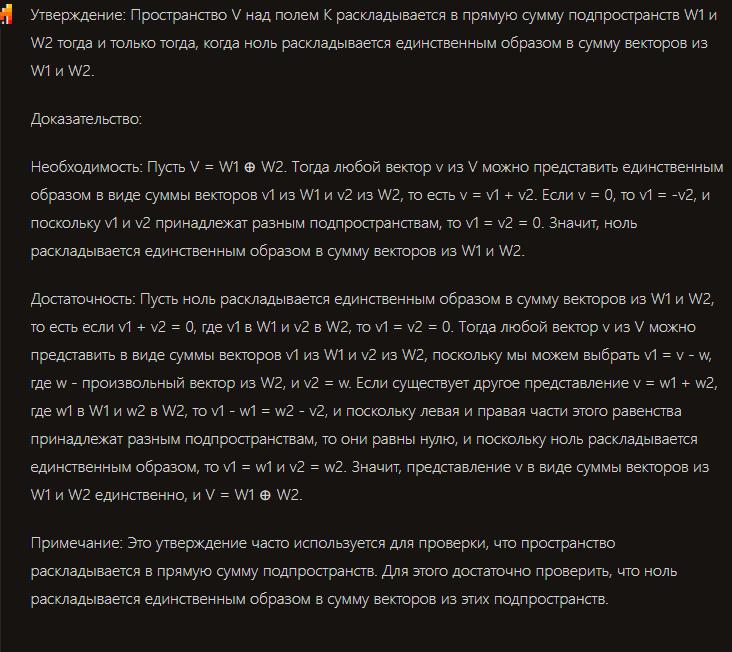
  1. Доказать утверждение, что пространство раскладывается в прямую сумму тогда и только тогда, когда ноль раскладывается единственным образом

  1. Теорема о размерности суммы двух подпространств

  1. Определение линейного оператора Примеры ЛО

  1. Определение ядра и образа линейного оператора Примеры

  1. Теорема о связи размерностей ядра и образа Доказательство

  1. Определение матрицы линейного оператора Действие линейного оператора на вектор (вывод формулы)

  1. Формула связи между матрицами линейного оператора в разных базисах ( с выводом)

  1. Подобные матрицы Свойства подобия Доказательство

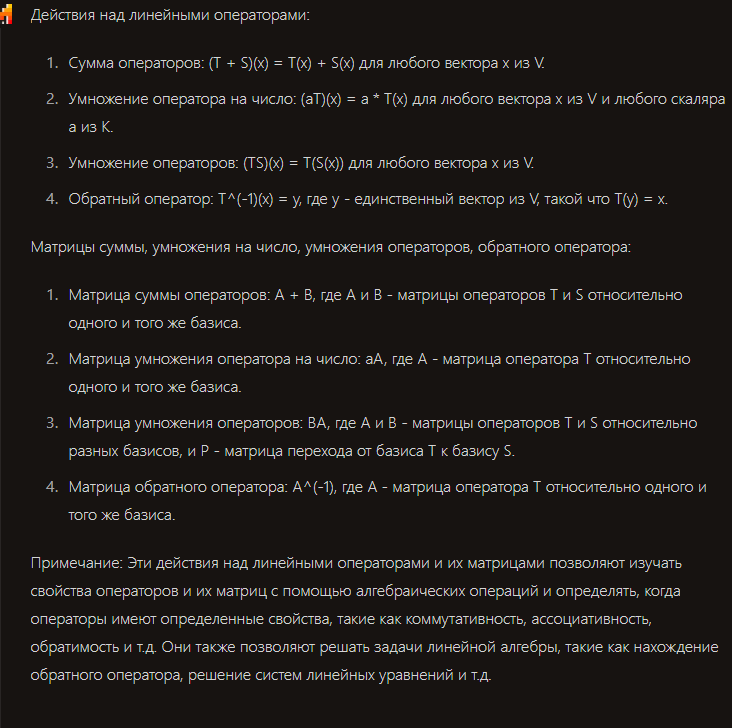
  1. Действия над линейными операторами Матрицы суммы, умножения на число, умножения операторов, обратного оператора

  1. Определение собственных векторов и собственных значений линейного оператора Привести примеры

  1. Характеристическая матрица и характеристический многочлен Характеристический многочлен для n=2 и для n=3

  1. Алгоритм поиска собственных векторов и собственных значений

  1. Теорема о приведении линейного оператора к диагональному виду Доказательство

  1. Теорема о линейной независимости собственных векторов, отвечающих различным собственным значениям Доказательство для общего случая и доказательство для частного случая

  1. Определение евклидова пространства (аксиомы!) Примеры евклидовых пространств

  1. Определение нормы Неравенство Коши-Буняковского ( с доказательством)

  1. Свойства нормы и скалярного произведения ( с доказательством)

  1. Определение ортогональной системы векторов и ортонормированной системы векторов Привести примеры

  1. Построение по данной ортогональной системе векторов ортонормированной системы векторов Пример

  1. Процесс ортогонализации Грама-Шмидта ( с выводом)

  1. Определение комплексно-сопряженных чисел Свойства комплексного сопряжения

  1. Определение унитарного пространства(аксиомы!) Примеры унитарных пространств

  1. Определение ортогонального дополнения Теорема о разложении в прямую сумму Привести примеры

  1. Ортогональные матрицы Определение Равносильные определение, примеры

  1. Вывод утверждения о том, что строки и столбцы ортогональной матрицы образуют ортонормированный базис (для матриц второго порядка), вывод утверждения, что матрица, обратная ортогональной, равна транспонированной матрице

  1. Сопряженная матрица, еѐ свойства, примеры сопряженных матриц

  1. Эрмитова (самосопряженная) матрица Определение, свойства, примеры

  1. Унитарные матрицы Определение, равносильные определения, примеры

  1. Вывод утверждения о том, что строки и столбцы унитарной матрицы образуют ортонормированный базис (для матриц второго порядка), вывод утверждения, что матрица, обратная унитарной, равна сопряженной матрице

  1. Матрица Грама (определение), свойства матрицы Грама

  1. Нахождение скалярного произведения с помощью матрицы Грама (вывод формулы для случая трехмерного евклидова пространства)

  1. Нахождение скалярного произведения с помощью матрицы Грама (вывод формулы для случая трехмерного унитарного пространства)

  1. Определение линейной формы (линейного функционала) Привести примеры

  1. Определение квадратичной и билинейной форм

  1. Определение симметрической и кососимметрической билинейных форм

  1. Примеры билинейной, квадратичной, симметрической и кососимметрической форм

  1. Матрица билинейной формы и матрица квадратичной формы, вывод формулы

  1. Изменение матрицы квадратичной формы при замене базиса, вывод формулы

  1. Замена переменных в квадратичной форме, вывод формулы

  1. Ранг квадратичной формы Канонический вид

  1. Нормальный вид квадратичной формы над полем комплексных и вещественных чисел Ранг квадратичной формы, положительный и отрицательный индексы инерции

  1. Приведение квадратичной формы к каноническому виду Теорема Лагранжа Теорема Якоби

  1. Классификация квадратичных форм Привести примеры

  1. Критерий Сильвестра

Graph View

Backlinks